Fast-track course on geometry for scientists and engineers.
Note: I recommend reviewing Part 1 and Part 2 before moving forward.
Geometric Properties of Shapes
Understanding the geometric properties of 2D and 3D shapes serves as the foundation for more advanced math topics such as calculus. Geometric properties of shapes are used on a daily basis in my experience at all the various jobs I worked as an engineer, and as such it is crucial to master these fundamentals. As a prerequisite for learning about shapes, first we will discuss coordinate systems.
Coordinate Systems
So far we have seen coordinates in x and y dimensions. This is referred to as the 2D Cartesian coordinate system, since the coordinate system axes are perpendicular to each other. We can also add another dimension z to have a 3D Cartesian coordinate system. However, this is not the only coordinate system we will encounter in engineering. Another 2D coordinate system we use is called the Polar coordinate system which uses dimensions of r and \theta , where r is radius and \theta is the angle.
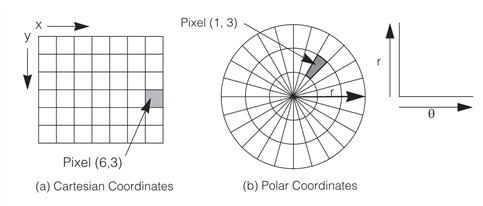
Sometimes it is easier to use one coordinate system over another one. For example, to draw a square it is more useful to use the Cartesian system, but to draw a circle it is more useful to use the Polar system. To convert between coordinate systems we must define one coordinate system in the units of the other system. Let’s explore how to derive this for Cartesian and Polar conversions. First, let’s place a sample point in space P and let’s superimpose both coordinate systems to define that point in both systems. Below shows the point in space (left) and the point with the Cartesian coordinates (x,y) in red and Polar coordinates (r,\theta) .
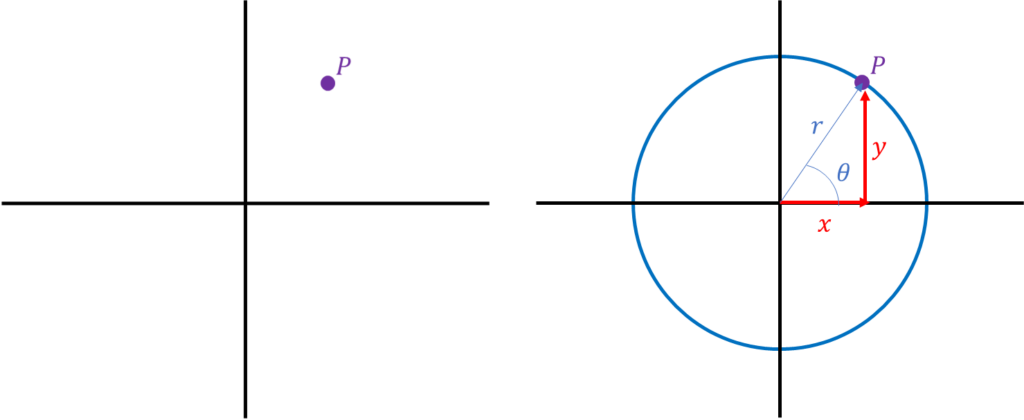
Upon closer inspection it is apparent that the shape formed by the two coordinate systems is a right triangle, so we can apply the trigonometry skills from the previous section to solve for the variables:
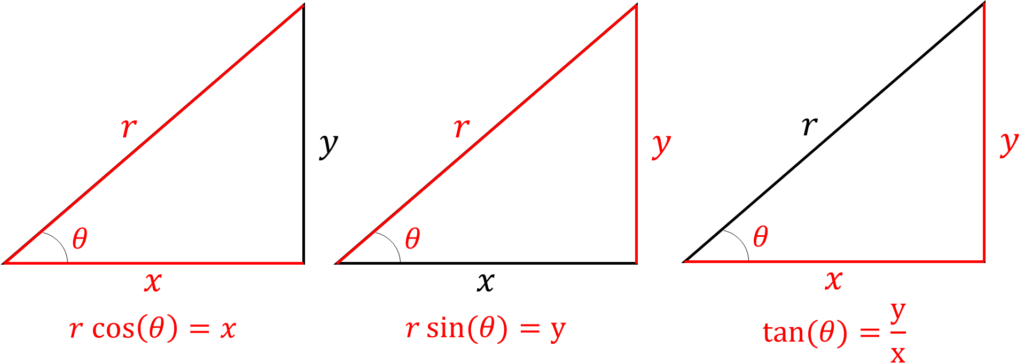
The conversion equations between Cartesian and Polar coordinates are given below:
x = r\cos(\theta)
y = r\sin(\theta)
\tan(\theta) = \frac{y}{x}
Using these equations we can now compute distance between two points. In Cartesian coordinates, the distance formula between two points (x_1, y_1), (x_2, y_2) is given by
\boxed{d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}}
Now, we can plug in the conversions to find the distance formula in Polar coordinates:
\boxed{ d = \sqrt{(r_2\cos(\theta_2) - r_1\cos(\theta_1))^2 + (r_2\sin(\theta_2) - r_1\sin(\theta_1))^2}}
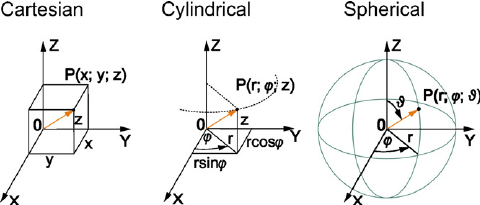
Similarly, in 3D we have other coordinate systems such as Cylindrical and Spherical coordinates shown below. Don’t worry if the 3D systems may seem complicated now. We will go more in depth in the Calculus articles.
2D Shapes
Shapes are created in mathematics by defining a function based on various variables. 2D shapes are shapes created on a plane of 2 dimensions (2 variables). We will commonly use X-Y planes to describe 2D shapes, however, any combination of 2 dimensions such as X-Z, Y-Z, or others. Similarly, 3D shapes are shapes created in a volume of 3 dimensions (2 planes or 3 variables) such as X-Y-Z.
Polygons
Polygons are 2D shapes formed by the closed circuit of 3 or more points joined by lines. These points are called vertices and the lines connecting them together are called edges. The simplest polygon is a triangle, which has 3 vertices and 3 edges. We already discussed how to compute the angles in the trigonometry section. However, we have yet to explore how to compute the area and perimeter of a triangle. The area of a triangle is the amount of space the interior takes up. This is calculated using the formula A = \frac{1}{2}bh , where b is the base of the triangle and h is the height:
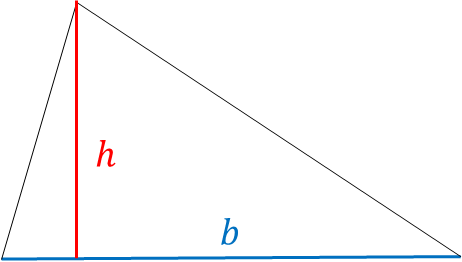
The perimeter of a triangle is length it takes to traverse the outside of the triangle. This is calculated by taking the sum of all the side lengths.
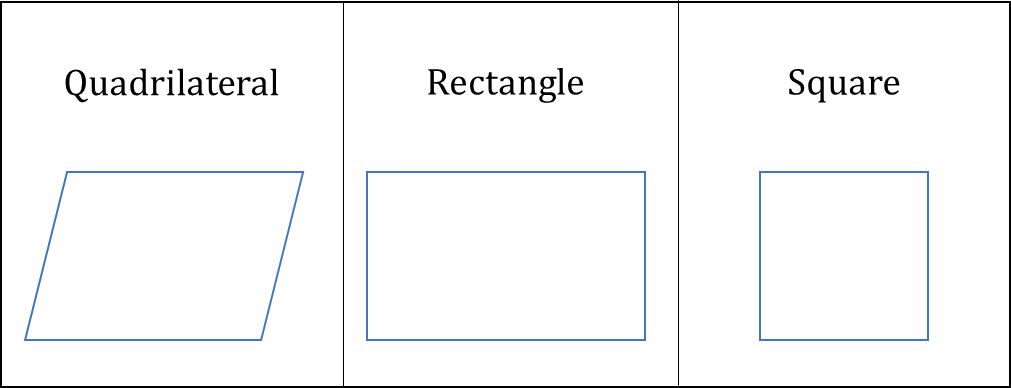
A triangle is a polygon with 3 sides. Therefore, the next shape we have is a quadrilateral, which is defined as a polygon with 4 vertices and 4 edges. A rectangle is defined as a quadrilateral with all right angles. A square is defined as a rectangle with all sides having equal length. The area of a quadrilateral is calculated by the following formula: A = bh . The perimeter is calculated again by summing all the side lengths together.
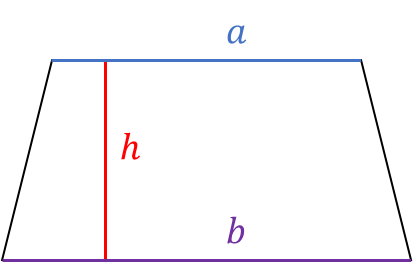
A special type of quadrilateral known as a trapezoid has an area of A = \frac{a+b}{2}h . This is given by taking the average of the two base lengths and multiplying that by the height.
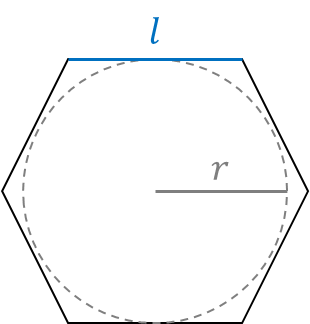
A generic polygon with n-number of sides is called an n-gon. For example, a polygon with 6 sides is called a hexagon because “hex” means 6. A polygon with 8 sides is called an octagon, and so forth. A regular n-gon is an n-gon with all sides equal length and all angles equal. The equation for the area of a regular n-gon is given by A = \frac{n}{2}lr where n is the number of sides, l is the side length, and r is the radius of the circle inscribed within the polygon (I will discuss the geometric properties of circles in the section below). The equation for the perimeter of a regular n-gon is given by p = nl .
Conics
Conic sections are a category of 4 main shapes formed by slicing a cone along various angles. The 4 shapes are parabolas, hyperbolas, ellipses, and circles (circles are a special case of ellipses).
Parabola
The general form of a parabola is given by the equation y = Ax^2 + Bx + C where A, B, C are constants. All the points on the parabola are equidistant, or the same distance, between a given fixed point, referred to as the focus, and a given fixed line, referred to as the directrix.
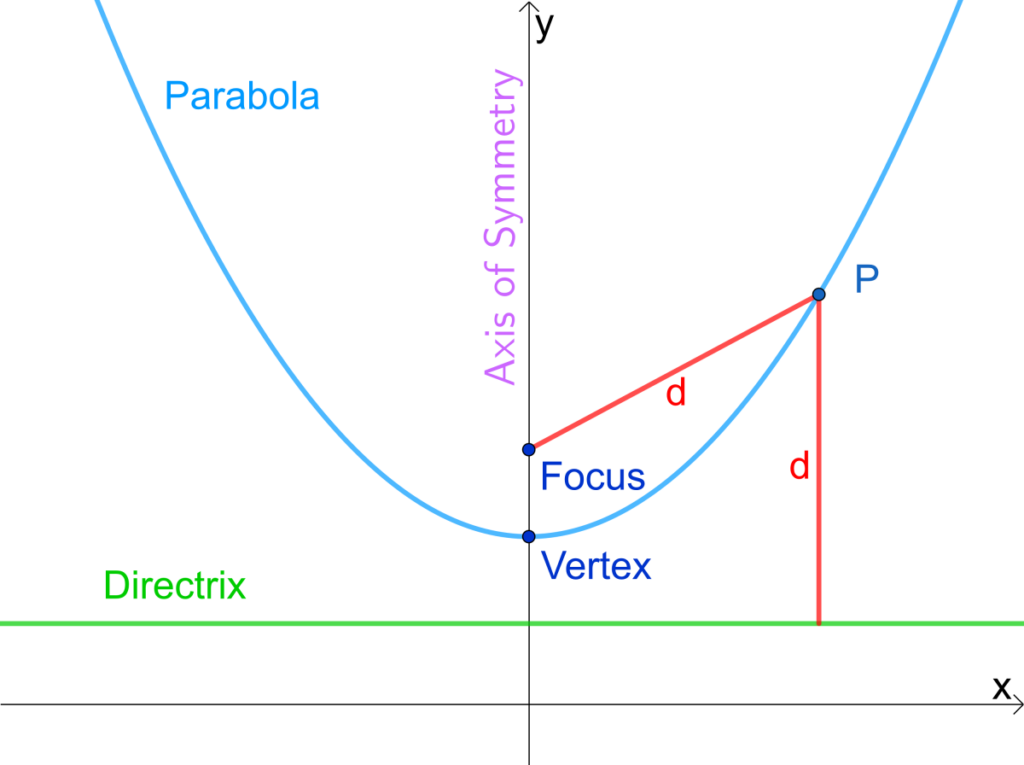
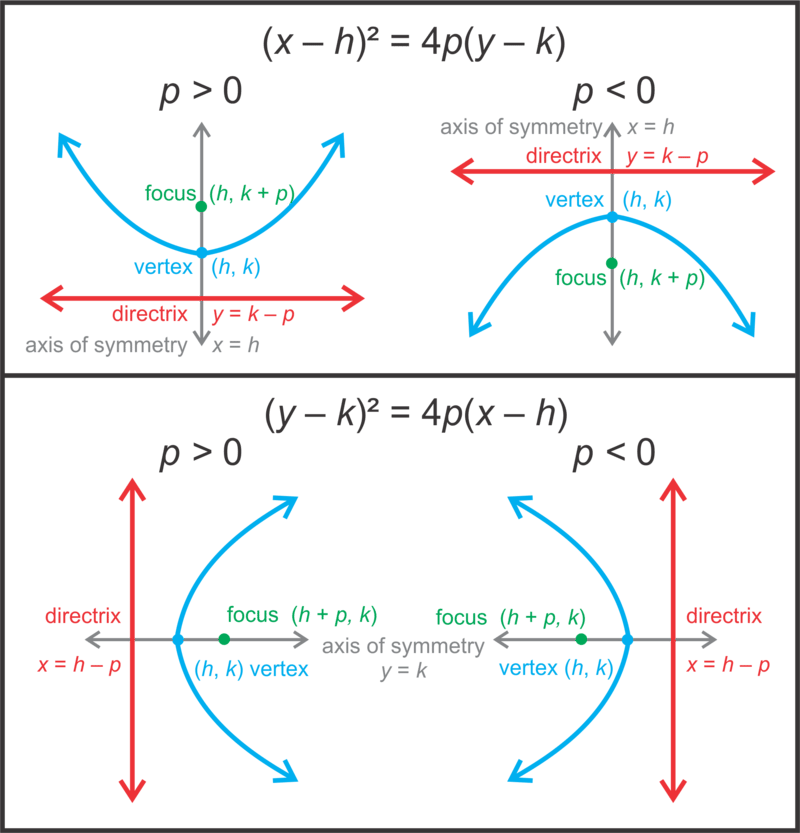
A more convenient way to write the equation for a parabola is the vertex form, which is given by y = \frac{(x-h)^2}{4p} + k where the point (h,k) is the point of the vertex of the parabola, (h,k+p) is the point of the focus, and y = k-p is the directrix line.
Hyperbola
A hyperbola is similar to a parabola, except it has two foci (plural of focus) and two directrices. It is a curve in which the difference between each point and both foci remains constant. The general form of the hyperbola equation is given by Ax^2 + By^2 + Cx + Dy + E = 0 where A, B, C, D, E are constants and A, B have opposite signs.
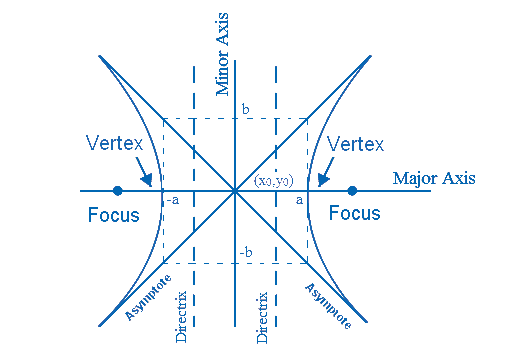
The standard form of the hyperbola equation is given by \frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1 where c^2 = a^2 + b^2 , (h,k\pm c) are the points of the foci, and y = k \pm \frac{a^2}{c} are the directrices lines.
Ellipse
An ellipse is similar to a hyperbola in that it has two foci and two directrices, except ellipses are defined as a curve in which the sum between each point and both foci remains constant. The general form of the ellipse equation is given by Ax^2 + By^2 + Cx + Dy + E = 0 where A, B, C, D, E are constants and A, B have same signs.
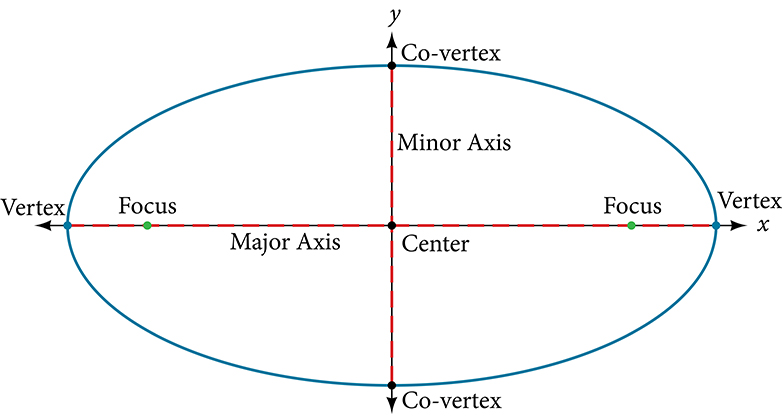
The standard form of the ellipse equation is given by \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 where c^2 = a^2 - b^2 , (h\pm c,k) are the points of the foci, and x = h \pm \frac{a^2}{c} are the directrices lines. The major axis the axis of the longer side and the minor axis is the axis of the shorter side.
The area of an ellipse is given by the equation A = \pi a b where a is the length of the major axis and b is the length of the minor axis. The perimeter of an ellipse is difficult to calculate exactly unless you know calculus, so it is beyond the scope of the geometry series. If you would like to learn more about finding the perimeter of an ellipse visit this article on mathisfun.
Circle
A circle is a special type of ellipse where both foci are at the center. The standard form of the circle equation is given by (x-h)^2 + (y-k)^2 = r^2 where the center of the circle is at the point (h,k) and the radius of the circle is given by r .
The radius of a circle is defined as the distance from the center of the circle to the outer edge. The diameter of the circle is defined as the distance from one end of the circle through the center to the other end of the circle.
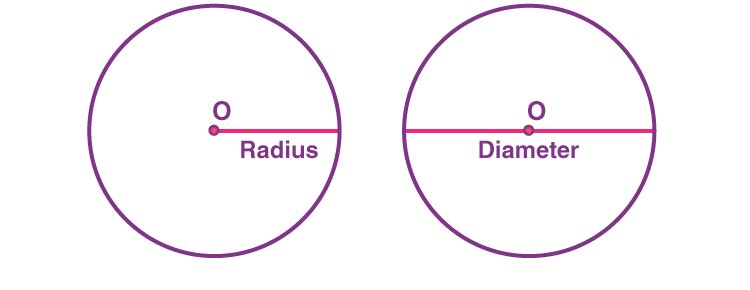
The area of a circle is given by the equation A = \pi r^2 . The circumference of a circle is the perimeter and is given by the equation c = 2\pi r .
Eccentricity
An important geometric property that is used to describe conic sections is eccentricity, which is defined to be the distance from any point on the conic section to its focus divided by the perpendicular distance from that point to the nearest directrix.
| Parabola | Hyperbola | Ellipse | Circle |
| e = 1 | e > 1 | 0 < e < 1 | e = 0 |
Now that we have covered the fundamentals of 2D shapes we can move on to the more complex 3D shapes.
3D Shapes
The most common geometric properties of 3D shapes you will be using as an engineer is volume and surface area. While calculus knowledge is required to compute each of these for any shape including irregular shapes, we will focus on the formulas for a few key common 3D shapes that you will encounter.
Prism
To compute the volume of a prism, multiply the area of the base by the length of the prism. To compute the surface area, find the areas of all faces of the prism and sum them all together. Below is a few examples of different prisms along with their volumes and surface areas.
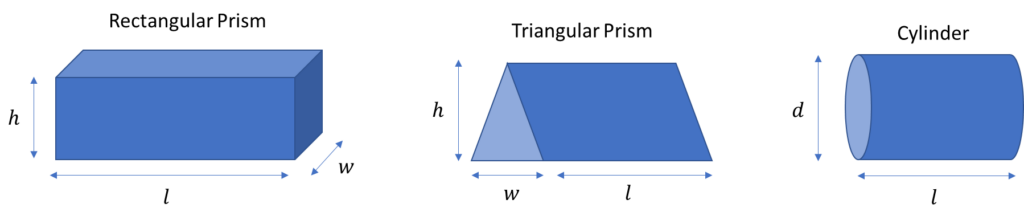
| Property | Rectangular Prism | Triangular Prism | Cylinder |
| Volume | V=whl | V=l\frac{hw}{2} | V= \frac{\pi}{4}d^2l |
| Surface Area | SA=2(wh+hl+lw) | SA=hw+3l\sqrt{h^2+\frac{1}{4}w^2} | SA=2\pi rl + 2\pi r^2 |
Miscellaneous Shapes
Some more common shapes you may encounter include pyramids, spheres, and cones. A summary of the equations for these other shapes are given below.
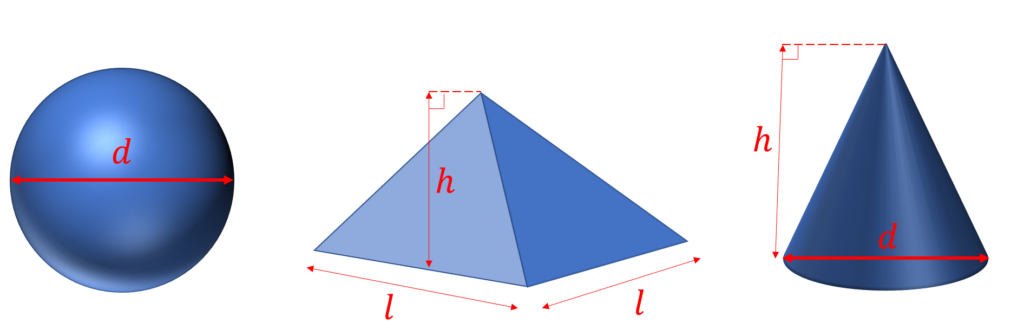
| Property | Sphere | Square Pyramid | Cone |
| Volume | V=\frac{\pi}{6} d^3 | V=\frac{1}{3}l^2h | V=\frac{1}{3}l^2h |
| Surface Area | SA=\pi d^2 | SA=2\left(l\sqrt{h^2+\frac{1}{4}l^2}\right) + l^2 | SA=\frac{\pi}{4}d^2 + \frac{\pi}{2}dh |