Fast-track course on geometry for scientists and engineers.
Note: I recommend reviewing Part 1 before moving forward.
Transversal Lines
A transversal line is a line that intersects two or more lines at distinct points. Transversal lines are frequently encountered in physics, especially in optics when calculating the path of lasers or rays of light. Knowing the rules governing the trigonometry of traversal lines is a valuable skill you will use throughout your study of engineering.
Let’s consider a sample case of a transversal line cutting through a pair of parallel lines:
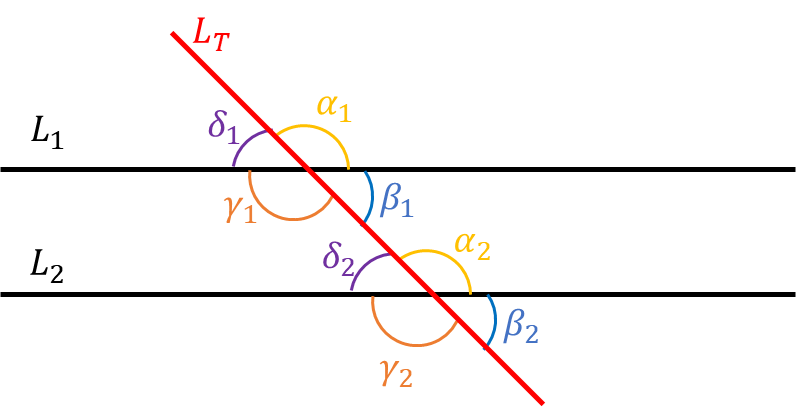
Since the lines L_1, L_2 are parallel (L_1 || L_2 ), this means that all the corresponding angles formed as a result of the transversal line L_T intersecting with line L_1 are equal to that of L_T intersecting with L_2 . Therefore, \alpha_1 = \alpha_2, \beta_1 = \beta_2, \gamma_1 = \gamma_2, \delta_1=\delta_2 . Note, that if any angles when summed together form a straight line, they are considered supplementary angles and add up to 180^\circ . Therefore, \begin{matrix}\alpha_1 + \beta_1 = 180^\circ \\ \beta_1 + \gamma_1 = 180^\circ \\ \gamma_1 + \delta_1 = 180^\circ \end{matrix} and these relationships are the same for the corresponding L_2 angles.
Alternate exterior angles are angles that are opposite to each other looking at the transversal cut from the outside. In this case, angles \delta_1 and \beta_2 are alternate exterior angles, as well as \alpha_1 and \gamma_2 . The Alternate Exterior Angles Theorem states that when a transversal intersects two parallel lines, the resulting alternate exterior angles are congruent, or equal in measure.
Alternate interior angles are angles that are opposite to each other looking at the transversal cut from the inside. In this case, angles \beta_1 and \delta_2 are alternate interior angles, as well as \gamma_1 and \alpha_2 . The Alternate Interior Angles Theorem states that when a transversal intersects two parallel lines, the resulting alternate interior angles are congruent, or equal in measure.
When solving transversal lines problems, always look for the alternate exterior and alternate interior angles to orient yourself then solve by setting up equations for the supplementary angles.
Example
Solve for the missing angle \beta .
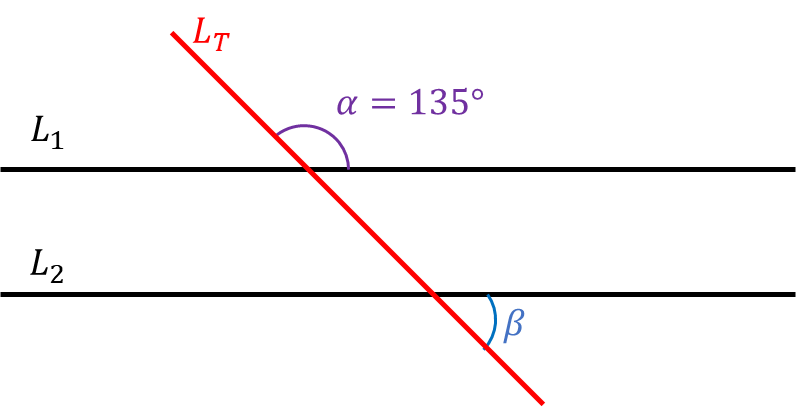
First, we need to identify that the angle \beta is the alternate exterior angle to the angle adjacent to \alpha . Therefore, if we solve for that angle, we arrive at our answer since it is congruent to \beta . Since \alpha + \angle = 180^\circ , we calculate the angle to be \angle = 45^\circ \therefore
\boxed{\beta = 45^\circ}
Next we will discuss the geometric properties of 2D and 3D shapes in Part 3.