Fast-track course on geometry for scientists and engineers.
Trigonometry
Trigonometry is a branch of mathematics dealing with solving for angles and dimensions of a shape. Trigonometry is crucial in science and engineering and is used in many applications including calculating forces using free-body diagrams, calculating the trajectory of projectiles, analyzing AC circuits, and much more. To delve into this subject, let’s first define what an angle is.
Angles
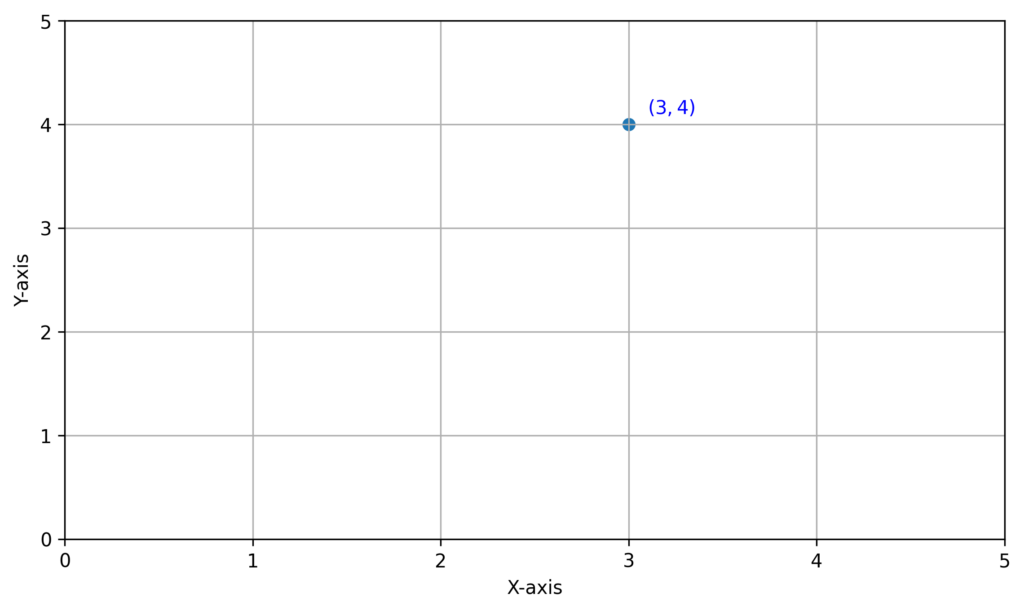
A point is a 1-dimensional position in space. It is written in the form (x, y) if working in 2D or (x, y, z) if working in 3D. We refer to it as a 1-dimensional position because a point defines a specific value to the x , y , and/or z variable, which is why we use parentheses to write them. To read a point and draw it on a graph, find the location at which the variables are defined. For example, the point (3,4) is read as x = 3, y = 4 . The following graph shows this point:
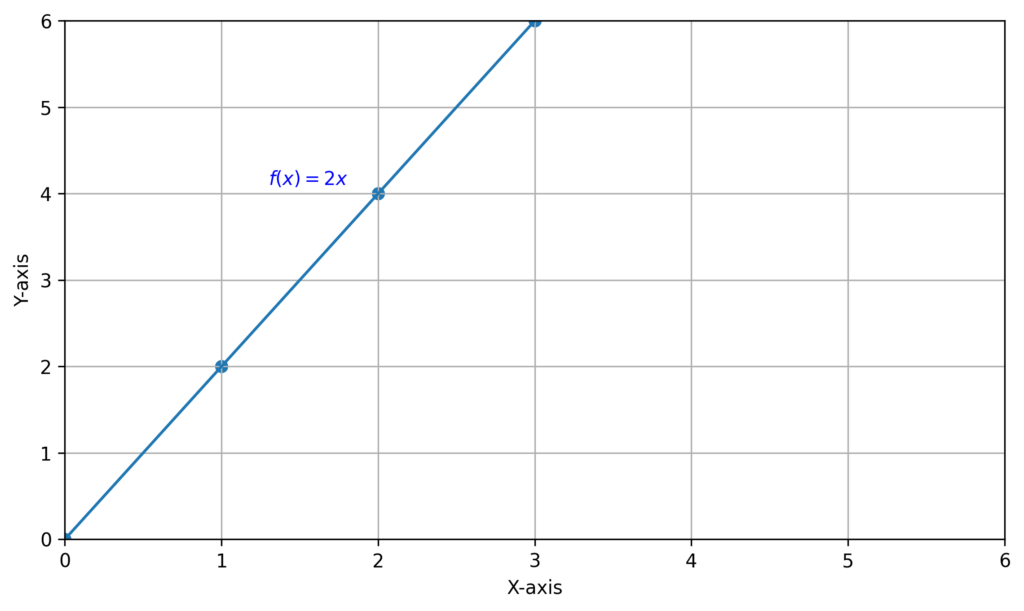
A line is a connection between any two points in space and is defined by a function. An example of a line is given by the function f(x) = y = 2x , which means for each x-value input the output is 2 times that input. Try plugging in different values for x and plot the corresponding f(x) value. See the table below for some sample points computed using this function and the corresponding graph of the line.
| x (Input) | f(x) (Output) |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
A ray is a line with a given direction, so that one end is pointing in one direction and the other is neutral. An angle is the union of two rays having a common endpoint. An angle can be measured in either degrees or radians. The conversion factor between the two is degrees=\frac{\pi}{180}radians , where \pi is a mathematical constant that is approximately equal to 3.14. A right angle is 90 degrees or \frac{\pi }{2} radians and is denoted by drawing a square bracket at the angle base. An acute angle is less than 90 degrees or \frac{\pi }{2} radians. An obtuse angle is greater than 90 degrees or \frac{\pi }{2} radians. A straight angle is 180 degrees.

Now that we have defined angles, lines, and points, we can move on to exploring the unit circle.
Unit Circle
In many science and engineering applications we deal with periodic functions, which are functions that take the form of \cos(x) (cosine), \sin(x) (sine), or \tan(x) (tangent). These functions are defined by the unit circle, which is a circle with a radius of 1 unit. The cosine of a particular angle value gives the distance along the x-direction of the circle, and the sine of the angle value gives the distance along the y-direction of the circle as shown below.
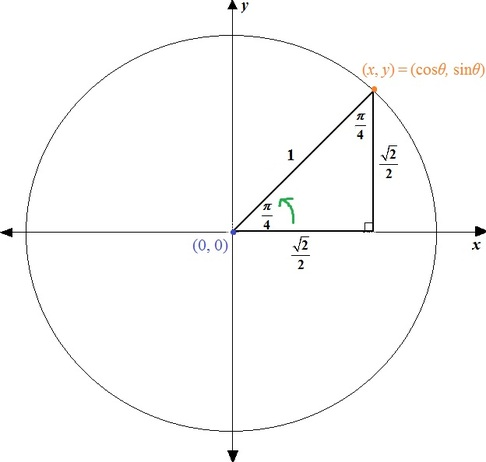
The tangent of an angle is defined as the ratio of the sine to the cosine \tan(x) = \frac{\sin(x)}{\cos(x)} . As you go along the circle from an angle of 0 degrees (0 radians) to the maximum angle of 360 degrees ( 2\pi radians), you will get the following values for the cosine and sine values:
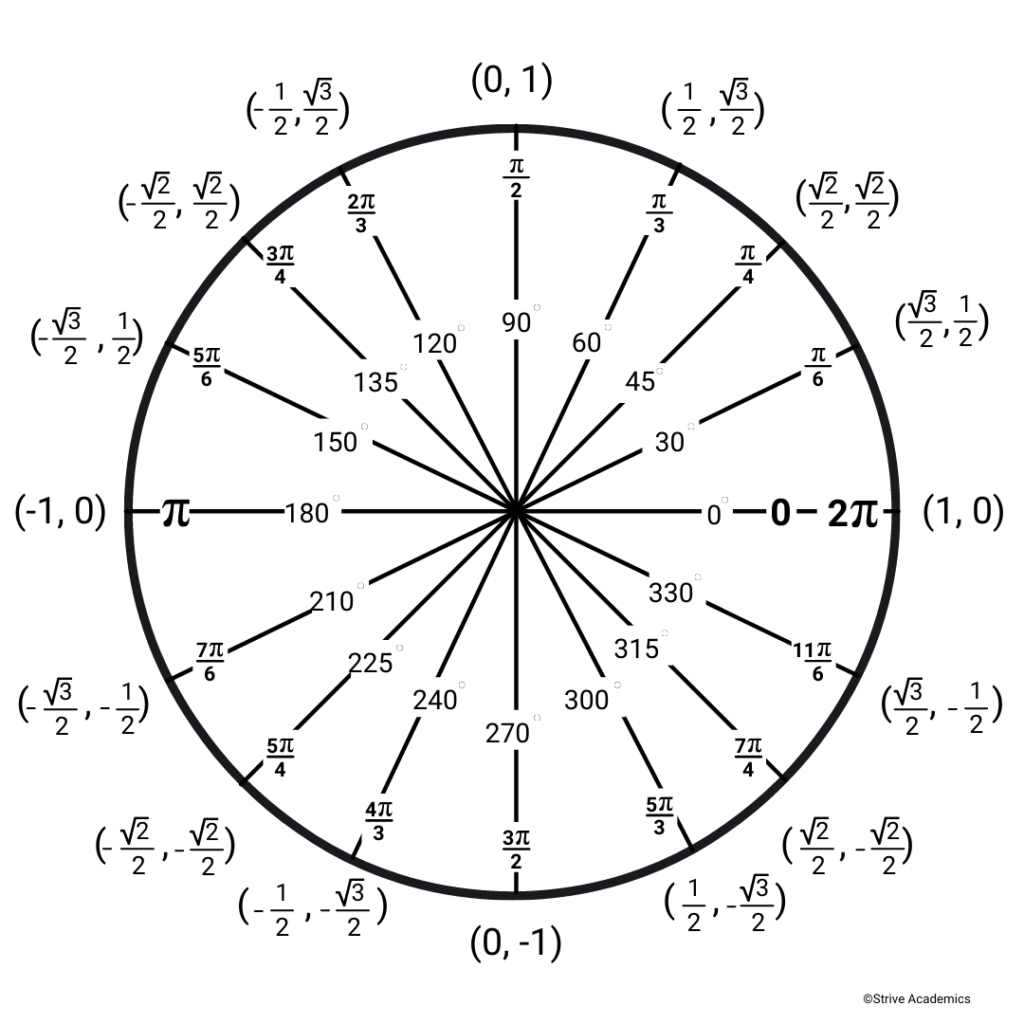
As you can see, for each point on the unit circle at a given angle, a triangle is formed as in the previous image. This is an important observation that we will utilize in the following section on solving unknowns in triangles.
Triangles
A closed shape of three or more points is defined as a polygon. A triangle is a polygon which consists of three points and the sum of all the angles amounts to 180 degrees or \pi radians.
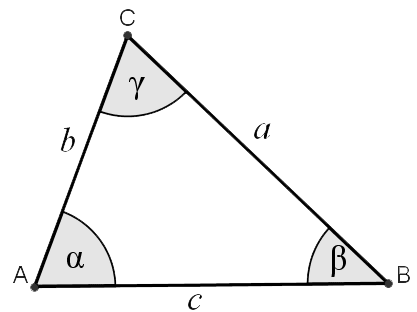
Right Triangles
A special type of triangle which we commonly encounter in science and engineering applications is the right triangle, in which one of the angles is equal to 90^\circ or \frac{\pi}{2} radians. A right triangle has two components, the legs and the hypotenuse. The hypotenuse is the side that is opposite of the 90^\circ angle and this is the longest side of the right triangle. The legs are the remaining two sides. This triangle is special because if we are given one side length and one angle, or two side lengths and no angles, we can solve for the rest of the sides and angles of the triangle using either sine, cosine, and tangent, or the Pythagorean theorem. The Pythagorean theorem states that for a right triangle the square of the side length of the hypotenuse is equal to the sum of the squares of the legs:
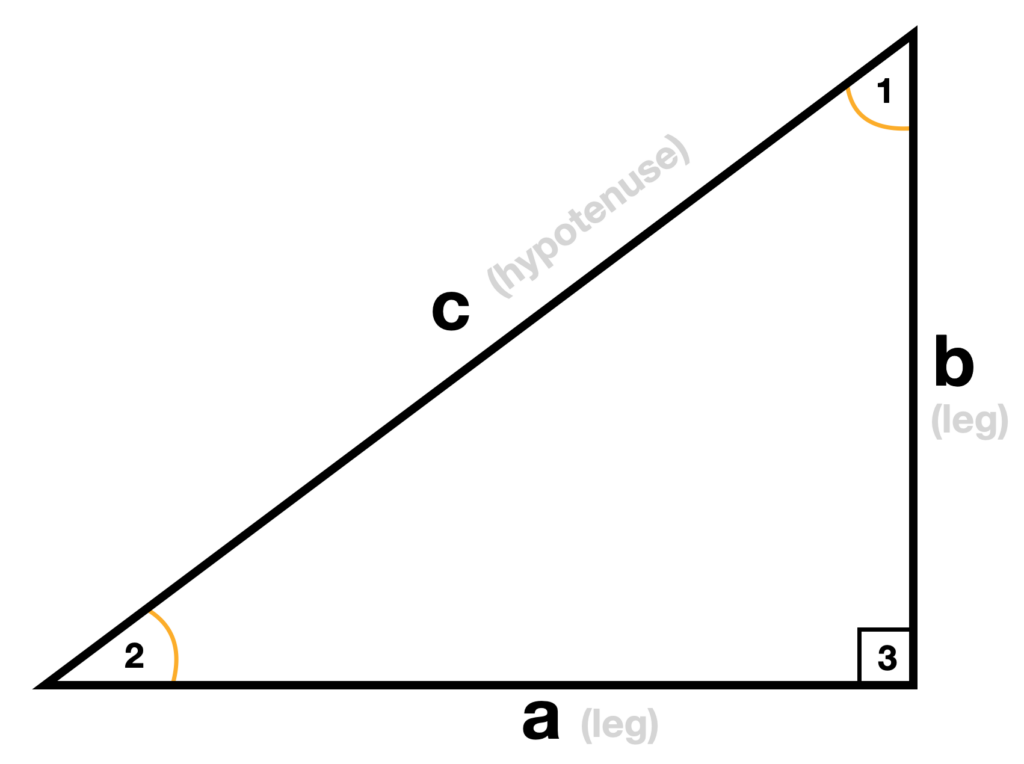
\boxed{c^2=a^2+b^2}
Example
Solve for the missing side of the following triangle using the Pythagorean theorem.
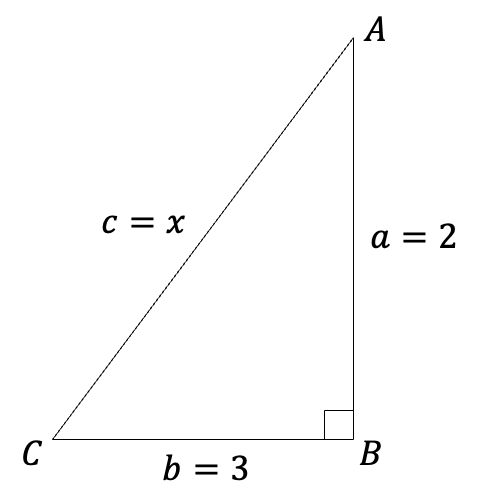
\begin{align*}c^2&=a^2+b^2\\ x^2&=2^2+3^2 \\ x &= \sqrt{2^2+3^2}\end{align*}
\boxed{c=x=\sqrt{13}}
To solve the triangle using sine, cosine, and tangent, we use the following properties:

| Sine | Cosine | Tangent |
| \sin(x)=\frac{Opposite}{Hypotenuse} | \cos(x)=\frac{Adjacent}{Hypotenuse} | \tan(x)=\frac{Opposite}{Adjacent} |
| \sin(\alpha)=\frac{a}{h} | \sin(\alpha)=\frac{b}{h} | \tan(\alpha)=\frac{a}{b} |
Example
Solve for the missing sides and the remaining angle of the following triangle using sine, cosine, or tangent.
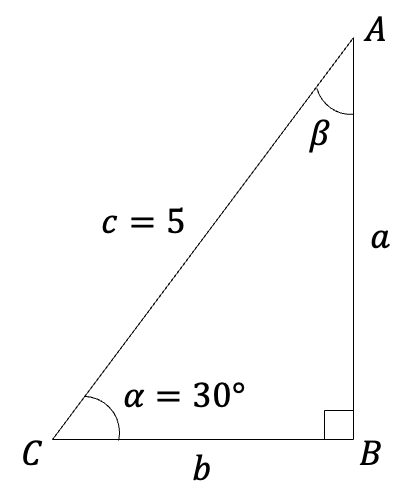
\begin{align*}\sin(30^\circ)&=\frac{a}{c}=\frac{a}{5}\\ a &= 5\sin(30^\circ)\end{align*}
\begin{align*}\cos(30^\circ)&=\frac{b}{c}=\frac{b}{5}\\ b &= 5\cos(30^\circ)\end{align*}
\begin{align*}\tan(\beta)&=\frac{b}{a} \\ \beta&=\arctan\left(\frac{b}{a}\right) \\ \beta&=\arctan\left(\frac{5\cos(30^\circ)}{5\sin(30^\circ)}\right) \end{align*}
\begin{matrix}a = 5\sin(30^\circ)\\ b = 5\cos(30^\circ)\\ \beta=\arctan\left(\frac{5\cos(30^\circ)}{5\sin(30^\circ)}\right)\end{matrix}
Plugging these values into a calculator gives the following solution:
\boxed{\begin{matrix}a = 2.5\\ b = 4.33\\ \beta=60\end{matrix}}
Check the answer by summing all the angles. If they sum to 180 degrees, then the answer is valid.
30^\circ+60^\circ+90^\circ \stackrel{\checkmark}{=}180^\circ
It is important to note that these relationships are only true for right triangles. For non-right triangles the problem is a slightly more complex.
Non-right Triangles
When working with non-right triangles (triangles which do not have any angles equal to 90^\circ ), we have two laws at our disposal which are universally applicable to both right and non-right triangles to help us solve for missing sides and/or angles – the Law of Sines and the Law of Cosines.
The Law of Sines states the following for a triangle with sides a, b, c and angles \alpha, \beta, \gamma :
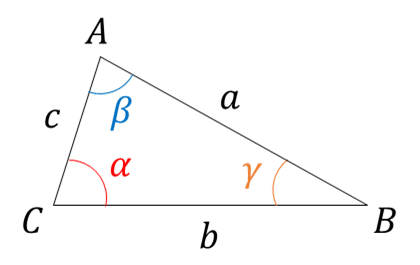
\boxed{\frac{\sin(\alpha)}{a} = \frac{\sin(\beta)}{b} = \frac{\sin(\gamma)}{c}}
Notice that the angle in the sine function in the numerator matches the side opposite to that angle. This is an easy way to remember the Law of Sines.
Example
Solve for the missing sides and the remaining angle of the following triangle using the Law of Sines.
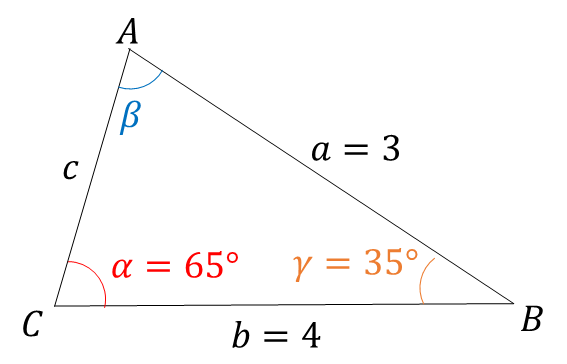
To make things easier, we can first notice that only one angle is missing, so we can apply the fact that all angles in a triangle must sum to 180^\circ \therefore \alpha + \gamma +\beta = 180^\circ \to \beta = 80^\circ . Next, we apply the Law of Sines to find the side c :
\frac{\sin(\alpha)}{a} = \frac{\sin(\beta)}{b} = \frac{\sin(\gamma)}{c}
\begin{align*} \frac{\sin(80^\circ)}{4} &= \frac{\sin(35^\circ)}{c} \\ c &= \frac{4\sin(35^\circ)}{\sin(80^\circ)} \\ c&= 2.33 \end{align*}
\boxed{ \begin{matrix} c = 2.33 \\ \beta = 80^\circ \end{matrix}}
The Law of Cosines states the following for a triangle with sides a, b, c and angles \alpha, \beta, \gamma :
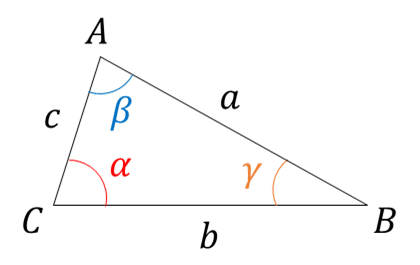
\boxed{\begin{align*} a^2 &= b^2 + c^2 - 2bc\cos(\alpha) \\ b^2 &= a^2 + c^2 - 2ac\cos(\beta) \\ c^2 &= a^2 + b^2 -2ab\cos(\gamma) \end{align*}}
Notice the similarity between this equation and that of the Pythagorean Theorem. Try applying the Law of Cosines formula to a right triangle. You will see that the term at the end will cancel out since the cosine of a right angle is zero, so it reduces to the Pythagorean Theorem in the case of a right triangle.
Example
Solve for the missing side of the following triangle using the Law of Cosines.
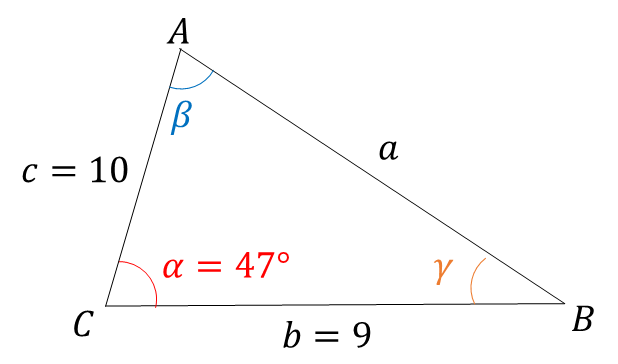
a^2 = b^2 + c^2 - 2bc\cos(\alpha)
a = \sqrt{81 + 100 - 180\cos(47^\circ) } = 7.63
\boxed{a = 7.63}
Now that you have a solid foundation in trigonometry, continue the lesson in Part 2 to apply what you learned to transversal lines problems.